
Applying Segmentation Methods In Geophysical Inversion to Improve The Recovery of Structural Features
Abstract¶
Geophysical inversions produce physical property models that are interpreted to provide geologic information. In this work, we leverage segmentation methods to promote the recovery of geologic structures in the inversion. The segmentation is incorporated into the inversion by adding a regularized segmentation as terms to the objective function. The Alternating Direction Method of Multipliers (ADMM) is used to solve the optimization problem. To demonstrate our approach, we present a synthetic DC resistivity example and an inversion of field MT data.
Introduction¶
Geophysicists interpret inversion models and communicate the results to non-geophysicists who make exploration decisions. We hope to answer geologists’ questions about the structural dip or where to expect to hit the mineralized zone. These questions can be challenging because geophysical inversions are non-unique and ill-posed. To approach this non-uniqueness, deterministic inversion approaches minimize an objective function consisting of a data misfit and model regularization term. The model regularization is often a combination of a smallness term that penalizes distance from a reference model, and a smoothness term that penalizes spatial gradients in the model. Within this framework, there are multiple approaches for incorporating prior information and producing inversion results that are more indicative of typical geologic structures. A-priori structural information about a target’s dip and orientation can be incorporated into the inversion by rotating derivatives in the smoothness term (Li & Oldenburg (2000)). Other methods promote clustering of the physical properties during the inversion, for example, Fuzzy c-means (Sun & Li (2017)) or the Petrophysically and Geologically guided Geophysical Inversion (Astic & Oldenburg (2019)). These approaches require that the user specify the number of rock units to be used in the clustering. In this work, we are motivated to explore how image segmentation can be used to improve the recovery of geologic features and to do so without having to specify the number of expected classes.
The work presented here builds upon previous work in which we developed an automated approach for inferring structural information during the inversion and incorporating this into the model regularization (Kuttai & Heagy (2024)). In our previous work, we used a pre-trained transformer network, SAM (Kirillov et al. (2023)), to perform image segmentation on the physical property model at a given iteration of the inversion and determine the primary orientation of each unit. The orientation information was then incorporated into the smoothness term of the regularization using the rotated-gradient approach of Li & Oldenburg (2000). We were using the segmentation only to infer orientations; however, this becomes limiting when structures are complex. In this work, we aim to include the segmentation directly into the inversion framework. To do so, we modify the statement of the inverse problem by adding a regularized segmentation to the objective function. We then use Alternating Direction Method of Multipliers (ADMM) to solve the optimization problem (Boyd et al. (2011)). ADMM breaks the problem into three steps: (1) a standard geophysical model update, (2) updating the segmentation, and (3) updating the constraint error term that connects the geophysical and segmentation update.
Related work by Ravasi & Birnie (2022) adapts the inverse problem to include a segmentation term in the objective function for seismic inversions. This work requires that the number of classes be predefined and held constant throughout the inversion. We extend the method by allowing the number of classes for the segmentation term to be adaptive and vary from iteration to iteration. We achieve this using the adaptive Gaussians technique from 3D image reconstruction methods like Gaussian splatting (Kerbl et al. (2023)). Our approach has the benefit that it produces a segmented model through the inversion, which may aid geologic interpretation. We illustrate that our approach improves the recovery of geologic structures using two examples. The first is a synthetic direct current (DC) resistivity example, and the second uses magnetotelluric (MT) data from the Athabasca basin of Saskatchewan, Canada.
Method and results¶
To incorporate segmentation into the inversion, we adapt the statement of the inverse problem to include two terms in addition to the usual data misfit () and model regularization (). Our approach is similar to Ravasi & Birnie (2022) except that we use a smoothness regularization on the physical property model instead of another total variation regularization. The first term that we add is which promotes the recovery of a physical property model that is close to the segmented model. The second term that we add, is a regularization on the segmentation itself. Our statement of the inverse problem is
where m is the physical property model vector, Z is a matrix of probabilities with each column containing the probability that a cell belongs to a class in c, and its shape is the number of cells by the number of classes ( by ). The vector c contains the classes, and its values are the mean of the physical properties of the cells associated with that class. are the trade-off parameters for each regularization term in the objective function. The first term of our objective function is the data misfit:
where ) is the forward model operator and is the observed data. The model regularization, if we choose to use one, is an L2 norm of the spatial derivatives of the model:
Here is a matrix containing the finite difference stencil and the multipliers that weight the smoothness term in each direction. The segmentation norm, which promotes similarity between the physical property of each cell and the class to which it is most closely associated, is represented by:
where is a probability element of matrix Z, and is the mean physical property of all cells belonging to that class. The nuance we add is that the number of classes is dynamically set. This allows for the classes to change at each iteration, adaptively. To achieve this, we use adaptive Gaussians that fit multiple Gaussians to the input model and add or merge the number of Gaussians that fit the input given splitting and merging thresholds. To regularize the segmentation, we use total variation regularization on each column of the matrix Z and then sum them. This controls how smooth or sharp the resulting segmentation is. We represent the total variation term as:
The objective function is now a complex optimization problem to minimize. ADMM lets us break up the problem and treat the data misfit and segmentation components separately. It then links both components with a coupling term. The full Lagrangian for our ADMM setup is:
where s is the segmentation model that has elements = for . The last term is the running constraint violation estimates; the difference between m and s at each iteration is summed cumulatively and stored in the vector u. The solution to the optimization problem using ADMM operates in 3 steps, as described by Boyd et al. (2010). First, we update the model according to
and Z, u are held constant. Then we update the segmentation
and m, u are held constant. Then, the errors are updated:
We iterate until we reach a target misfit and then continue to iterate further until the changes in the constraint are below a set threshold.
To illustrate our approach, we first apply it to a synthetic model. In this example, we include the smoothness for the m update. We simulate a DC resistivity survey collecting pole-pole and pole-dipole measurements with parameters a=25m to 250m and n=16. The synthetic model contains an intrusive dipping conductor and two shallow, horizontal, faulted layers (Figure 1a). The standard L2 recovered model, shown in Figure 1b, is smooth, and the dip of the intrusive unit is recovered as a more steeply dipping feature than it should be. The geophysical model recovered using the segmentation approach (Figure 1c), resolves the horizontal layering and improves the dip estimate of the intrusive conductor. The segmentation model derived from Z is shown in Figure 1d, and it captures the geological features rather well. We can see the two shallow horizontal layers, the intrusive conductor, and we see the influence of the fault near x=150m as the top layer thickened. There is also a vertical offset between the most resistive units recovered as the dark blue units in Figure 1d.
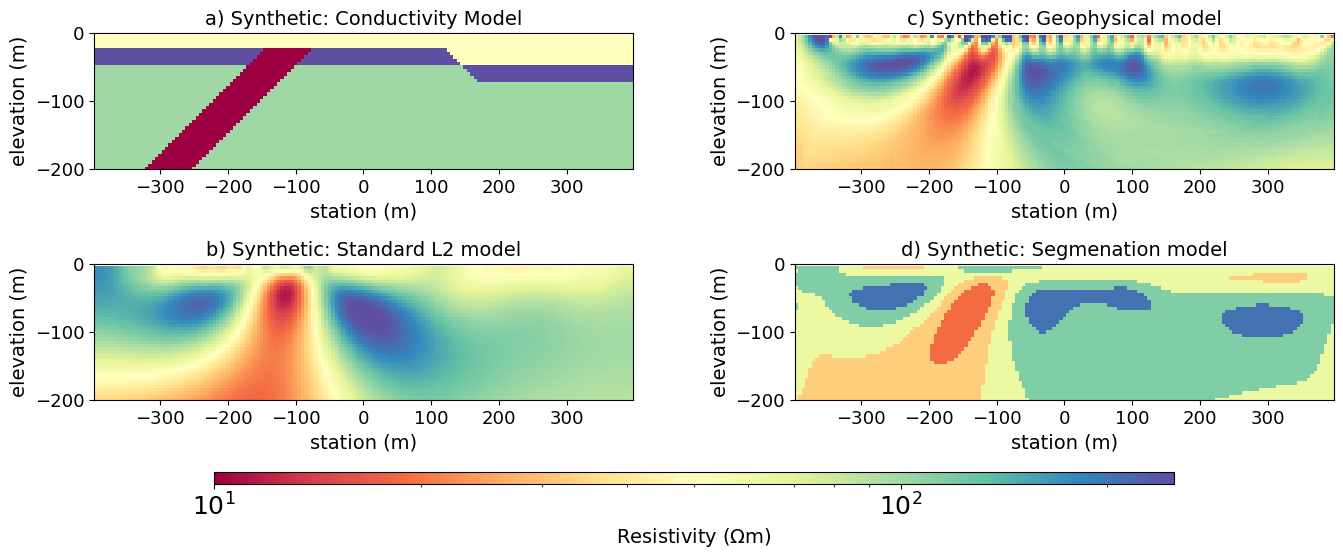
Figure 1:Recovered model comparison when using segmentation and standard L2 methods for inversion. The data is a DC-resistivity simulation over a synthetic conductivity model illustrated in (a). The standard L2 result is shown in (b), while the recovered geophysical model with the regularized segmentation added to the objective function is shown in (c). The auxiliary space Z is used to produce the recovered segmentation model shown in (d).
The field example we demonstrate uses magnetotelluric data to target graphitic conductors that form in the faulted unconformity in the Athabasca basin of Saskatchewan, Canada. For this example, the smoothness term for the m update is excluded. The standard L2 shown in Figure 2a indicates two conductors that are not distinctively defined, and the dip of each is ambiguous. By adding a regularized segmentation to the objective function as described above, we recover a geophysical model that has two distinct conductors (Figure 2b). Figure 2c shows the segmentation model derived from matrix Z by assigning each cell the physical property with the highest probability. The two conductors recovered have been explored extensively, and the conductor near 521,000m is the P2 conductor, which hosts the McArthur River Mine’s uranium deposits (Tuncer (2007)).
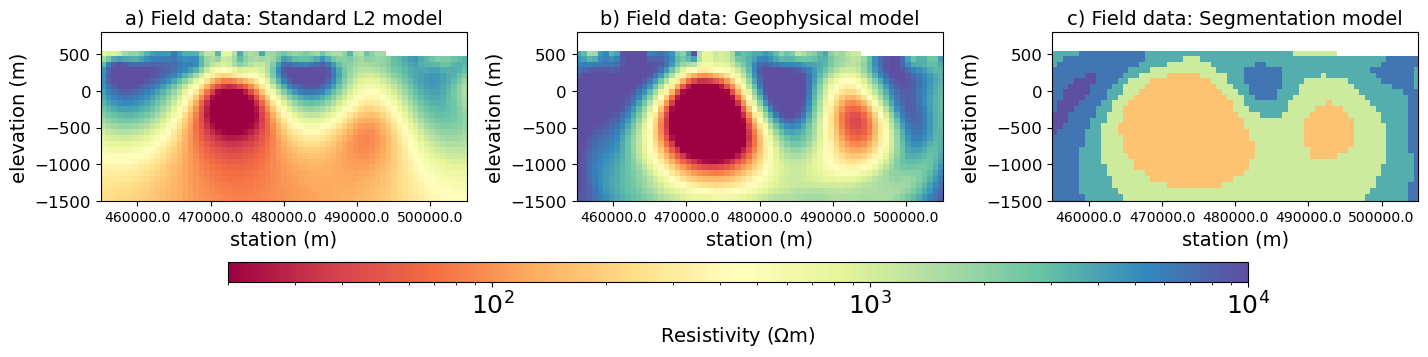
Figure 2:Recovered model comparison using magnetotelluric field data targeting dipping basement graphitic conductors. The standard L2 recovered model is shown in (a). The recovered geophysical model output from ADMM is shown in (b), and the corresponding segmentation model in (c)
Conclusions¶
We have introduced an inversion approach that leverages segmentation algorithms. Our work incorporates the segmentation into the inversion by adding a regularized segmentation to the objective function. ADMM provides a mathematical framework to encode segmentation directly into the inversion process. However, this approach introduces an additional term along with hyperparameters that control the influence of segmentation on the inversion result. Developing reliable strategies for assigning these values is an avenue for future research. Unlike other clustering-based inversion methods, our approach does not require specifying the number of classes beforehand, as this value is dynamically updated throughout the inversion process. This contribution provides the tools to recover models that can be more geologically interpretable. In particular, we show that in the synthetic example, we are able to distinguish multiple layers and improve the dip estimate of the intrusive conductive dyke. In the MT field example, we recover two distinctive, conductive targets that are coincident with the known P2 fault and a second grouping of faults.
Copyright © 2025 Kuttai & Heagy.
- ADMM
- Alternating Direction Method of Multipliers
- DC
- Direct-current
- MT
- Magnetotelluric
- Li, Y., & Oldenburg, D. W. (2000). Incorporating geological dip information into geophysical inversions. Geophysics, 65, 148–157. 10.1190/1.1444705
- Sun, J., & Li, Y. (2017). Joint inversion of multiple geophysical and petrophysical data using generalized fuzzy clustering algorithms. Geophysical Journal International, 208, 1201–1216. 10.1093/gji/ggw458
- Astic, T., & Oldenburg, D. W. (2019). A framework for petrophysically and geologically guided geophysical inversion using a dynamic Gaussian mixture model prior. Geophysical Journal International, 219, 1989–2012. 10.1093/gji/ggz402
- Kuttai, J. C., & Heagy, L. J. (2024). An automated approach to incorporate structural information into the inversion using image segmentation. EAGE Near Surface Geophysics Conference and Exhibition.
- Kirillov, A., Mintun, E., Ravi, N., Mao, H., Rolland, C., Gustafson, L., Xiao, T., Whitehead, S., Berg, A. C., Lo, W. Y., Dollár, P., & Girshick, R. (2023). Segment Anything. arXiv preprint arXiv:2304.02643. https://arxiv.org/abs/2304.02643
- Boyd, S., Parikh, N., Chu, E., Peleato, B., & Eckstein, J. (2011). Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning, 3, 1–122. 10.1561/2200000016
- Ravasi, M., & Birnie, C. (2022). A joint inversion-segmentation approach to assisted seismic interpretation. Geophysical Journal International, 228, 893–912. 10.1093/gji/ggab410
- Kerbl, B., Kopanas, G., Leimkühler, T., & Drettakis, G. (2023). 3D Gaussian Splatting for Real-Time Radiance Field Rendering. arXiv preprint arXiv:2308.04079. https://arxiv.org/abs/2308.04079
- Tuncer, V. (2007). Exploration for Unconformity-Type Uranium Deposits with Audio-Magnetotelluric Data: A Case Study from the McArthur River Mine, Saskatchewan, Canada [Master’s Thesis]. University of Alberta.
